原题链接
力扣87
大意是给定两个字符串,是否可以通过对其中一个字符串不断分裂、交换获得第二个字符串。
思路
第一次尝试暴力,脑补了一下觉得不太能写的出来(其实这个时候感觉可以动归,但是只能想到简单的记录状态),看了题解之后恍然大悟,发现还是一道值得一提的题目。
我认为比较好的做法就是官方题解中给出的做法,也就是动态规划。看看要素:
- 子问题重叠性。显然,两个子串是否可以最终等价是状态,这样的状态会被重复计算;
- 最优子结构。本题属于可行判断,故而如果两个子串是否匹配被计算出来,其必然就是最后的结果;
- 无后效性。显然是满足的。
接下来看状态、阶段以及决策。
状态已经提及了,简单说来就是两个子串以及匹配的长度,官方题解中将其简化成了一个<i,j,len>的三元组(将原字符串当成成员变量,类似于全局变量)。
阶段和决策,常见的处理方法是push(使用一个状态去更新其他状态)或者pull(从其他状态更新当前的状态)。本题实际上更适合第三种方法——记忆化搜索。记忆化搜索就是在暴力搜索的过程中记录已经访问过的状态,避免重复访问(bfs里也有类似的思想)。本题由于具有递归的结构,使用记忆化搜索也是很好写的。如何决策?这其实就是本题的状态转移方程是什么。这里直接使用官方题解给出的图示:
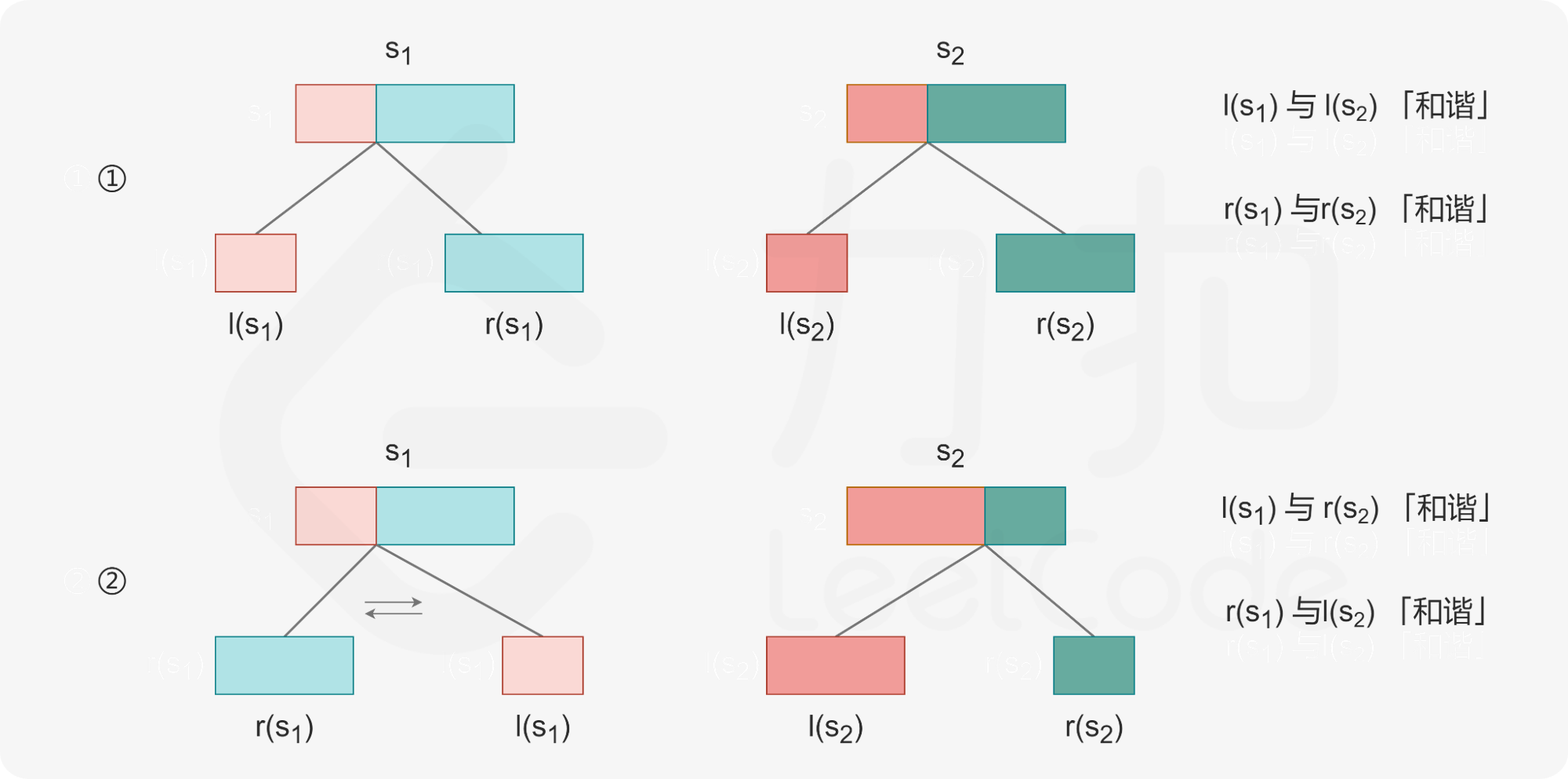
一图胜千言,简单说来,就是交换或者不交换,对于每一种状态,枚举中间节点即可。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
| class Solution {
public:
string s1;
string s2;
int vis[31][31][31];
bool isMatched(int i1,int i2, int length){
unordered_map<char,int> hash;
for(int i = 0;i<length;i++){
hash[s1[i1+i]]++;
hash[s2[i2+i]]--;
}
return !any_of(hash.begin(), hash.end(),[&](const auto& e){return e.second!=0;});
}
bool dfs(int i1, int i2, int length){
if(vis[i1][i2][length]){
return vis[i1][i2][length] == 1;
}
if(s1.substr(i1,length)==s2.substr(i2,length)){
return vis[i1][i2][length] = 1;
}
if(!isMatched(i1,i2,length)){
vis[i1][i2][length] = -1;
return false;
}
for(int k = 1;k<length;k++){
if(dfs(i1,i2,k) && dfs(i1+k, i2+k, length-k)){
return vis[i1][i2][length] = 1;
}
}
for(int k = 1;k<length;k++){
if(dfs(i1+length-k,i2,k) && dfs(i1,i2+k,length-k)){
return vis[i1][i2][length] = 1;
}
}
vis[i1][i2][length] = -1;
return false;
}
bool isScramble(string s1, string s2) {
memset(vis,0,sizeof(vis));
this->s1 = s1;
this->s2 = s2;
return dfs(0,0,s1.size());
}
};
|
感谢阅读!欢迎评论嗷~
